AMC10|圆中的角度与长度

大家知道AMC是美国数学竞赛American Mathematical Competition的简称。1950 年美国数学协会Mathematics Association of America （简称MAA），开始举办美国高中数学考试（AHSME）。在1985年时，MAA又增加了初中数学的考试（AJHSME），2000年以后这些考试统一 被称为 AMC，AMC总部现设在美国加州內布拉斯加大学林肯校区。AMC考试包括AMC8、AMC10、AMC12、AIME、USJMO、USAMO。今天amc数学竞赛网小编就和大家说一说AMC10|圆中的角度与长度：

圆是一个不难画出的图形，一笔就能画出来。但圆却是一个比较难理解的图形，因为它是一个曲线图形。

我们所学的“长度”、“面积”这些量的计算，最初都是在直线图形上定义的。比如：两点间的距离就是两点连成线段的长度；一个图形的面积就是长乘宽。

但是曲线的长度和曲线图形的面积怎么理解呢？这是一个比较深奥的问题，讲这个问题之前，咱们先来看看圆的基本性质：

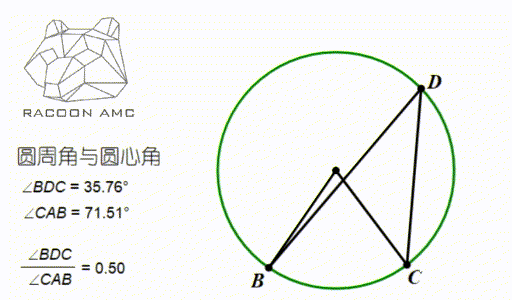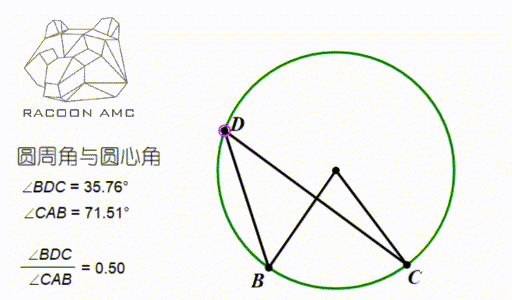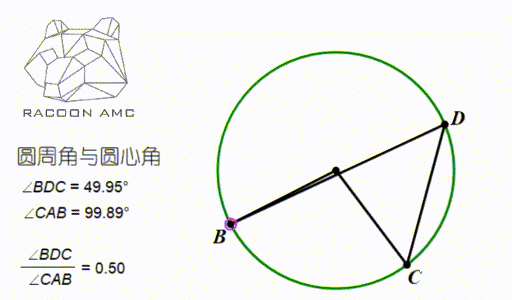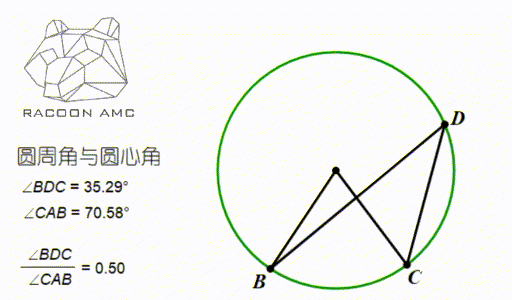
圆上的一段弧的两个端点于圆周上一点连线所成的角，叫做圆周角（Circumference Angle），如图中∠BDC；

圆上的一段弧的两个端点于圆心连线所成的角，叫做圆心角（Center Angle），如图中∠BAC

圆的一个重要性质就是：

同弧所对的圆周角相等，且等于圆心角的一半。

一条弧 BC有唯一确定的圆周角与之对应，但一条弦 BC就有两个圆周角与之对应。这是什么意思呢？我们来看下一个例子。

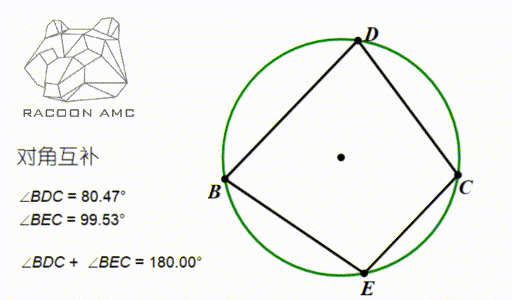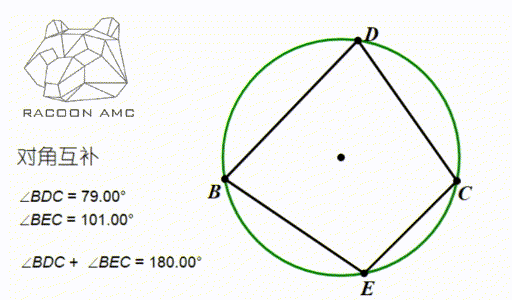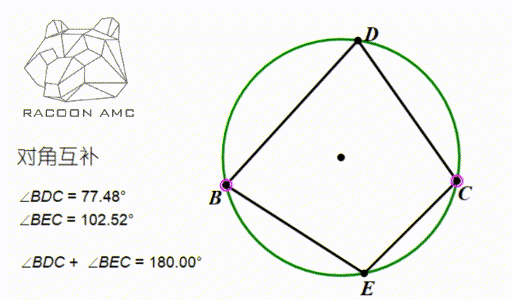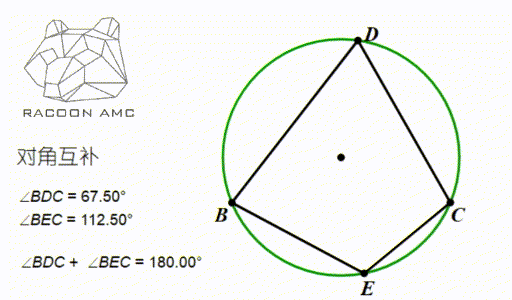
如图中∠BDC 和∠BEC ，他们都是 BC 这条弦所对的圆周角，他们分别在 BC 所在直线的两侧。数量关系是：互补。于是这个性质可以总结为：圆内接四边形对角互补。

由这个性质，我们可以推出一个重要的角度相等关系，如下图

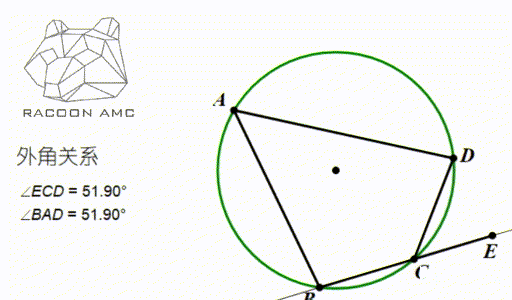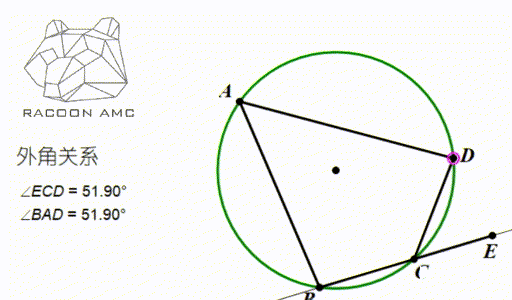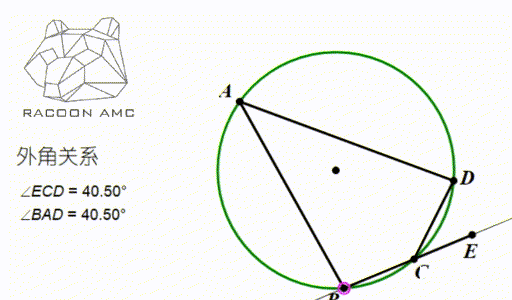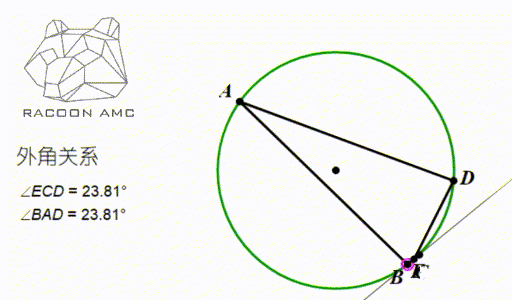
圆内接四边形外角等于内对角。

它的一个极端形式（即图中 B和C 无限靠近的时候）是：弦切角等于这条弦所对的圆周角。

刚才说完了角度关系，咱们再来说说长度关系。

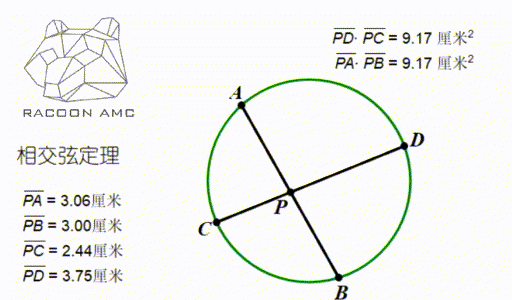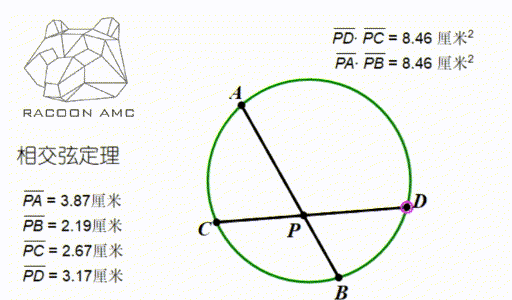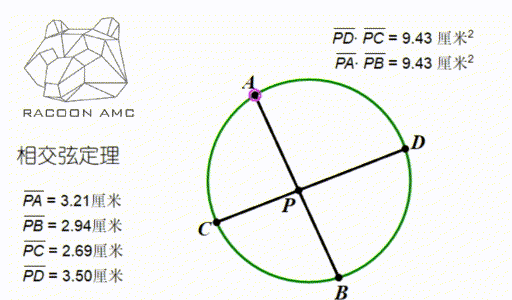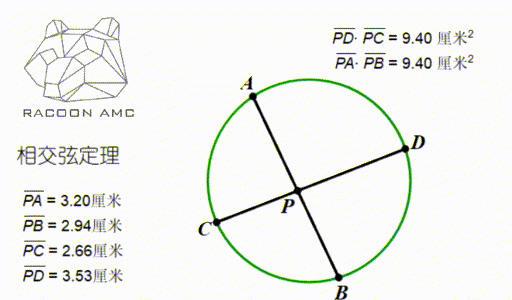
如上图，在圆中，AB 和 CD 是两条相交的弦，交点为 P，那么长度就具有这样的关系

PA×PB = PC×PD

这个定理叫做相交弦定理，可以用三角形 PAC 和三角形 PDB 相似来证明。

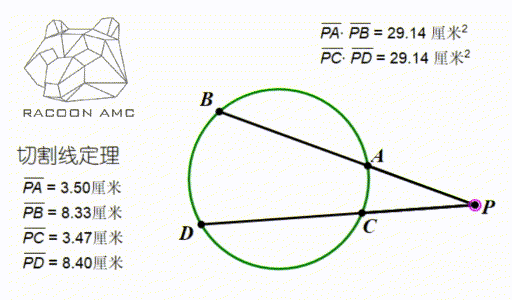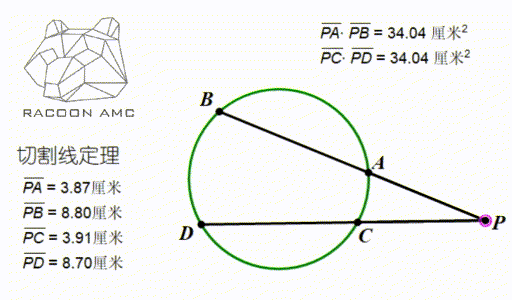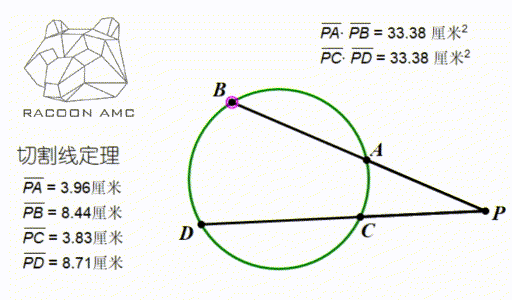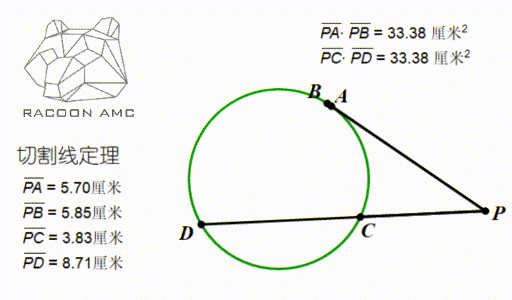
如果 P 点在圆外，引两条圆的割线，那么依然有这个数量关系：PA×PB=PC×PD，这个定理叫做切割线定理（如图，当 A、B 无穷靠近的时候 PA 就成了切线），这个定理也是用三角形 PAC 和三角形 PDB 相似来证明。

相交弦定理和切割线定理合称圆幂定理 （Power of Points formula）

让我们回到最初的问题，圆形作为一个曲线图形，它面积和周长到底怎么与由直线定义的长度面积过渡过来的？曲线的长度和曲线图形的面积怎么理解呢？

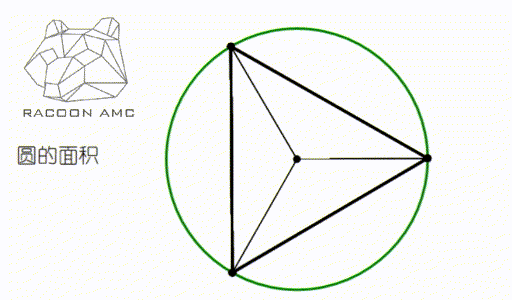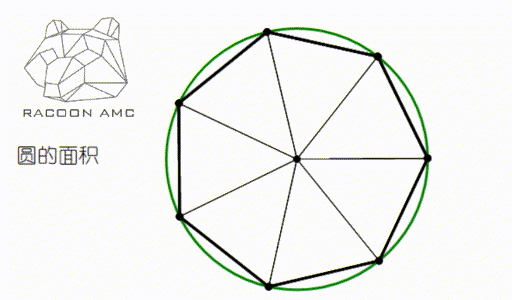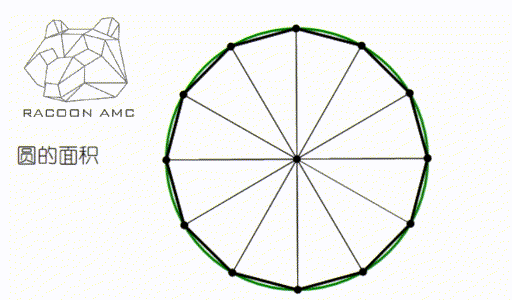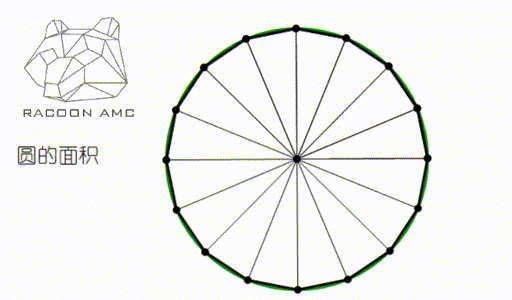
大家仔细观察上图就明白了，圆可以看成多边形的边数不断增加，趋于无穷的结果。很多关于 π 的公式都由此而来。不过这就不是中学数学需要深究的了，大家在大学将会接触到。

以上就是小编对AMC10|圆中的角度与长度的介绍，希望对你有所帮助，更多学习资料请持续关注AMC数学竞赛网！