AMC8|平行四边形及其好兄弟们

1950 年美国数学协会Mathematics Association of America （简称MAA），开始举办美国高中数学考试（AHSME）。在1985年时，MAA又增加了初中数学的考试（AJHSME），2000年以后这些考试统一 被称为 AMC，AMC总部现设在美国加州內布拉斯加大学林肯校区。AMC考试包括AMC8、AMC10、AMC12、AIME、USJMO、USAMO。今天amc数学竞赛网小编就和大家说一说AMC8|平行四边形及其好兄弟们：

平行四边形，大家肯定都很熟悉，但是你知道吗？它可是好几位小弟的大哥，只有跟大哥搞好关系，你才能和各位小弟友好相处。

四边形可以分三类：

①两组对边都不平行的：这种一般比较难，暂不研究

②只有一组对边平行的：叫做梯形 （trapezoid）

③两组对边都平行：叫做平行四边形（parallelogram），咱们现在就来具体说说它

由对边平行这个定义出发，我们很快就能推出它的另一些基本性质：

①对边相等

②对角相等

③对角线互相平分

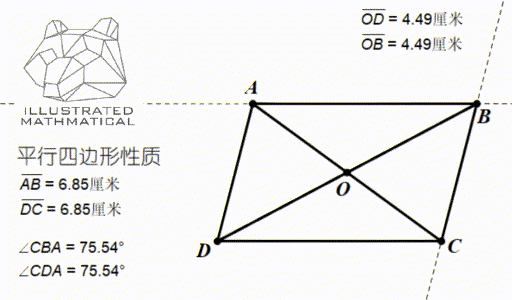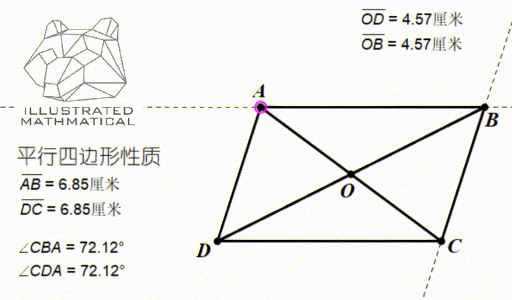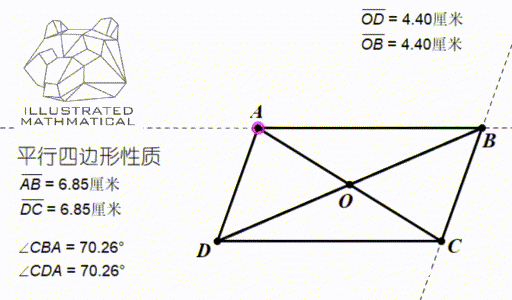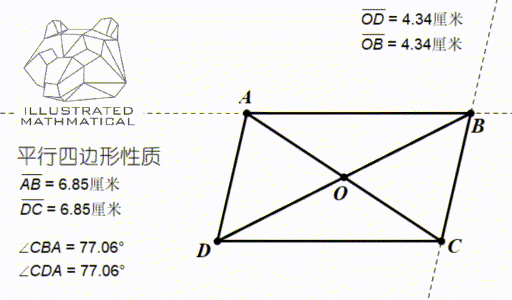
以上三条性质都可以用全等三角形来证明。

下面我们来看一个课内不常接触到的性质，对角线长度和边长的关系：

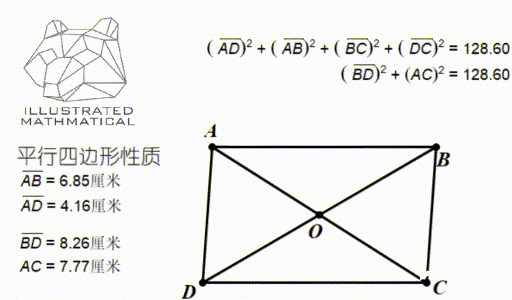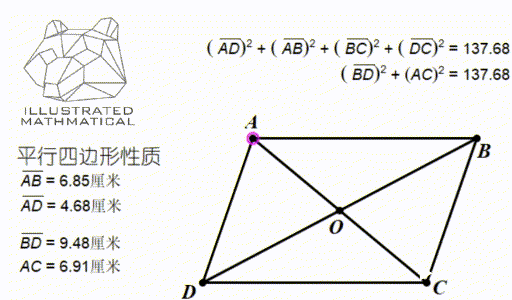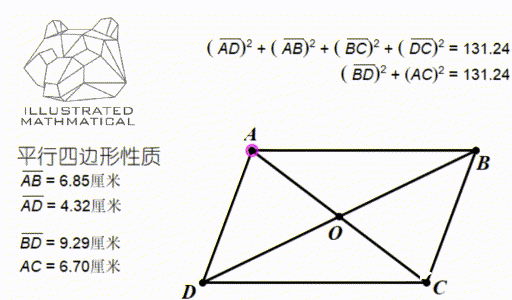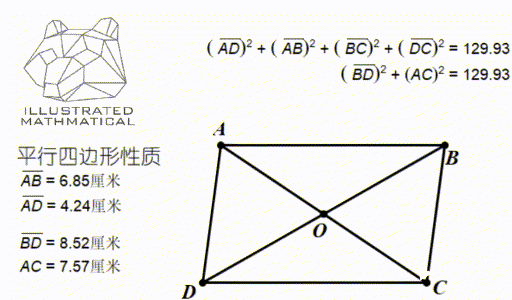
观察上图，我们发现，四条边长的平方和等于两条对角线的平方和。

当你知道平行四边形两条对边和其中一条对角线的长度的时候，就能用这个性质快速算出另一条对角线长度。

这个性质最简单的推导是用余弦定理来计算两条对角线长度，两式相加得出。

我们知道，平行四边形的面积是底乘高，这个公式是怎么推导出来的呢？

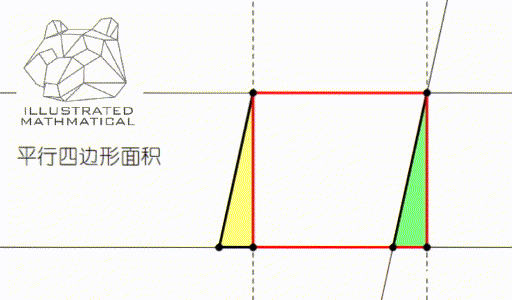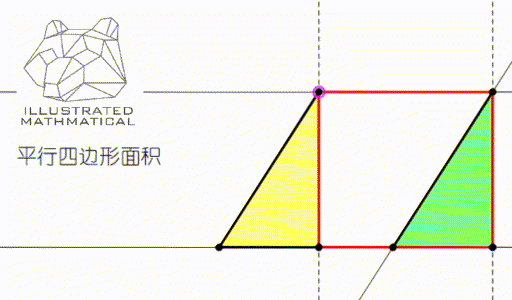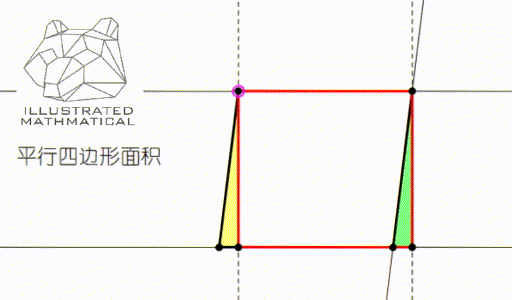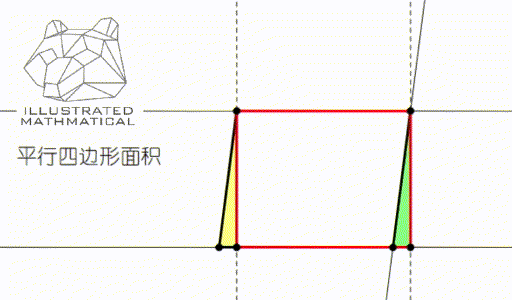
观察上图我们可以发现，无论平行四边形是什么形状的，我们总可以剪下黄色的三角形，把它拼到绿色三角形的地方，这样平行四边形的面积就可以用长方形面积公式——长乘宽来算了。

如上图，平行四边形被两条对角线分成四个三角形，上下两个三角形全等，左右两个三角形也全等，有趣的是，虽然上面的三角形和右边的三角形不全等，但它们面积一样。

证明方法可以是：CA=AF， D 到底边 CA 和 AF 的距离也相等，于是两三角形面积相等。

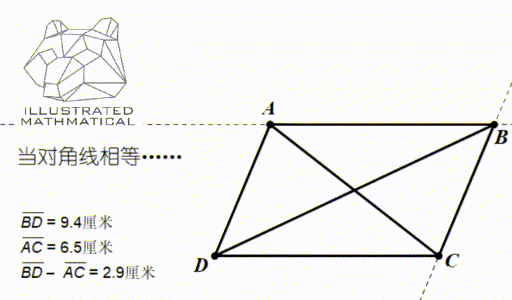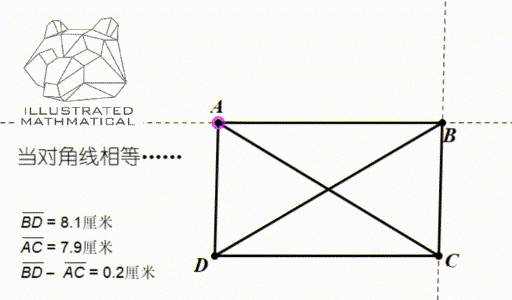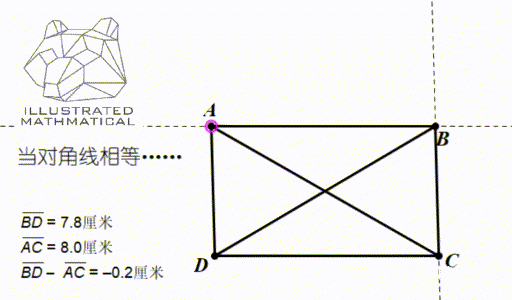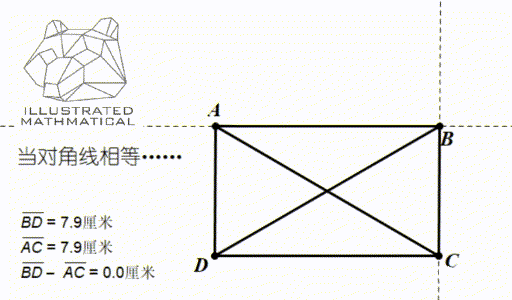
一般情况下，平行四边形两条对角线是不相等的，但通过调整，使得两条对角线长度相等，大家来想想会发生什么呢？

观察图形变化，我们发现，当对角线相等的时候，平行四边形恰好变成了长方形！所以，矩形是平行四边形的第一个小弟。

这个性质可以由全等三角形证明，它对应两条定理：

①对角线相等的平行四边形是矩形

②矩形的对角线长度相等

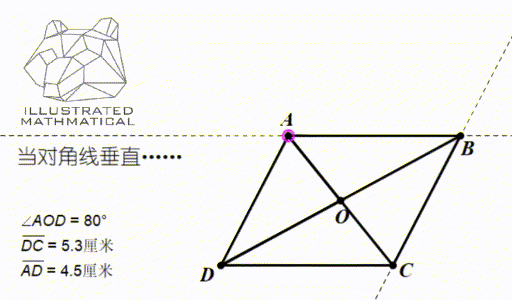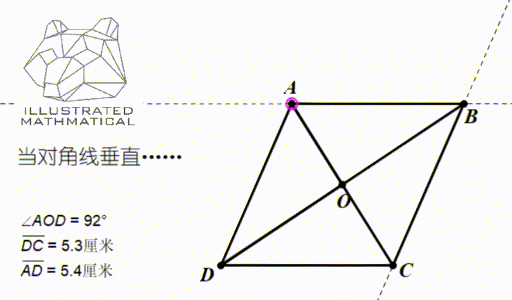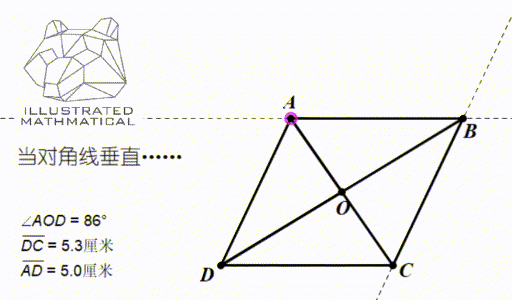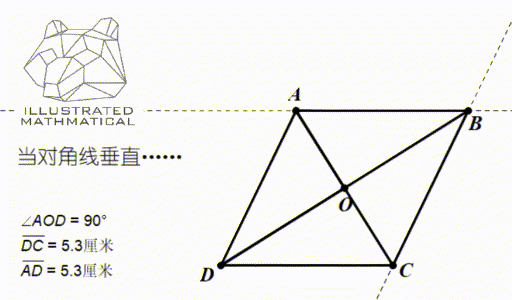
以上两条互为逆定理。一般情况下，平行四边形两条对角线是不垂直的，但通过调整，使得两条对角线垂直，大家来想想会发生什么呢？

观察图形变化，我们发现，当对角线垂直的时候，两条邻边长度就相等了，平行四边形恰好变成了菱形（rhombus）！所以菱形是平行四边形的第二位小弟。

这个性质依然可以由全等三角形证明，它对应两条定理：

①对角线垂直的平行四边形是菱形

②菱形对角线相互垂直

以上两条互为逆定理

最后说一句，如果一个图形既是矩形又是菱形，那么它就是我们最常见的正方形了。正方形平行四边形的第三位小弟。

以上就是小编对家长应该如何为孩子规划AMC数学竞赛的介绍，希望对你有所帮助，更多学习资料请持续关注AMC数学竞赛网！